Probability for Machine Learning:Conditional Probability
Conditional probability is a concept that helps us to understand how the likelihood of an event changes when we have some information about another related event. For example, suppose you want to know the probability of getting a head when you toss a coin. If you have no information about the coin, you might assume that the probability is 50%, since there are two equally likely outcomes: head or tail. However, if you know that the coin is biased and has a 70% chance of landing on the head, then the probability of getting a head is no longer 50%, but 70%. This is an example of conditional probability, where the probability of an event (getting a head) depends on the condition (the coin is biased).
How to calculate conditional probability?
To calculate conditional probability, we need to use a formula that relates the probability of the event of interest (called the conditional event) and the probability of the condition (called the given event). The formula is:
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
where P(A|B) means the probability of A given B, P(A∩B) means the probability of both A and B happening together, and P(B) means the probability of B happening.
The formula can be understood intuitively by thinking of a Venn diagram. Suppose we have two events A and B that are represented by two circles that overlap. The overlap area represents the event A∩B, which means both A and B happen. The circle for B represents the event B, which means only B happens. The ratio of the overlap area to the circle for B is the same as the ratio of the probabilities of these events, which is the conditional probability of A given B.
Examples of conditional probability
Let's look at some examples of how to use conditional probability in real-life situations.
Example 1: Rolling a die
Suppose you roll a fair six-sided die and want to know the probability of getting a 6 given that you get an even number. In this case, the event A is getting a 6 and the event B is getting an even number. To use the formula, we need to find:
P(A|B): the probability of getting a 6 given that you get an even number
P(A∩B): the probability of getting both a 6 and an even number
P(B): the probability of getting an even number
We can find these probabilities by counting the possible outcomes:
There are 3 possible outcomes for getting an even number: 2, 4, or 6. So, P(B)=1/2
There is only 1 possible outcome for getting both a 6 and an even number: 6. So, P(A∩B)=1/6
Using the formula, we get:
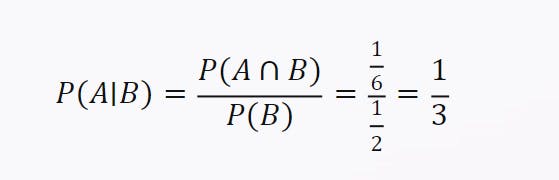
The probability of getting a 6 given that you get an even number is 1/3.
Example 2: Drawing cards
Suppose you have a standard deck of 52 cards and want to know the probability of drawing an ace given that you draw a red card. In this case, the event A is drawing an ace and the event B is drawing a red card. To use the formula, we need to find:
P(A|B): the probability of drawing an ace given that you draw a red card
P(A∩B): the probability of drawing both an ace and a red card
P(B): the probability of drawing a red card
We can find these probabilities by counting the possible outcomes:
There are 26 possible outcomes for drawing a red card: 13 hearts and 13 diamonds. So, P(B) = 1/2
There are 2 possible outcomes for drawing both an ace and a red card: ace of 1/26
Using the formula, we get:
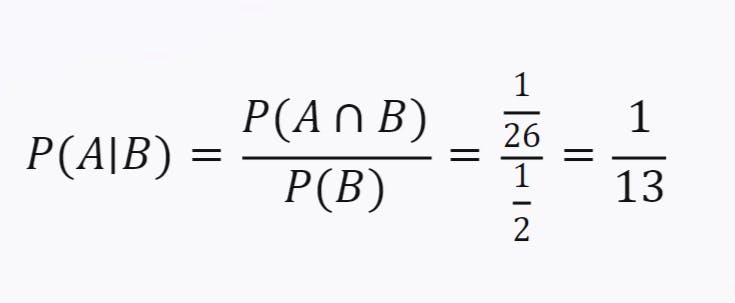
The probability of drawing an ace given that you draw a red card is 1/13
Conclusion
Conditional probability is a useful tool to measure how the likelihood of an event changes when we have some information about another related event. It can be calculated by using a formula that involves the probability of both events happening together and the probability of the given event. Conditional probability can be applied to many real-life situations, as shown in the blog. However, conditional probability can also be affected by factors such as bias, false positives, false negatives, and accuracy of tests. Therefore, it is important to understand the assumptions and limitations of conditional probability before using it to make decisions.
Hope you got value out of this article. Subscribe to the newsletter to get more such updates, and please feel free to provide any feedback on the blogs.
Thanks :)
